Az ismert vírusok jelentős részének ikozaéder alakú a fehérjeburka. Ez a gömbszerű, eredetileg húsz háromszögű lapból álló, szabályos test számos evolúciós előnyre tett szert. Egy frissen megjelent tanulmányban[1] Tyukodi Botond és kutatótársai azt vizsgálták, hogy milyen építőelemekből lehet a legegyszerűbben és leghatékonyabban nanostruktúrákat létrehozni. A vírusokéhoz hasonló, ikozaéderes héjak összeszerelődését modellezve megmutatták, hogy a nanovilágban léteznek az úgynevezett varázslatos méretek, amelyek esetében az ikozaéder héj összeszerelődéséhez szükséges alkatrészek száma radikálisan lecsökken. Ez nemcsak a vírusok számára jelent evolúciós előnyt, hanem a nanotechnológia számára is utat mutat a hatékonyabb, spontán összeálló rendszerek tervezéséhez. A BBTE-n oktató fizikussal Serestély Zalán beszélgetett a Physical Review Letters-ben megjelent tanulmány apropóján.
Serestély Zalán: A frissen megjelent tanulmányotok több tudományterület metszéspontján helyezkedik el: biológia, orvostudomány, anyagtudomány, számítógépes modellezés, statisztikus fizika. A CV-dből az derül ki, hogy már a mesteri tanulmányaid alatt foglalkoztatott a számítógépes fizika. Mi az, ami vonzóvá teszi számodra ezeket a metszéspontokat?
Tyukodi Botond: A számítógépes modellezés valóban az egyetemi tanulmányaim alatt kezdett el foglalkoztatni, akkori tanáraim (mostani kollégáim) hatására. Azelőtt biztos voltam benne, hogy teljesen alkalmatlan vagyok a legegyszerűbb algoritmus kifejlesztésére és leprogramozására is, de ők a gondosan felépített kurzusokon és laborokon meggyőztek az ellenkezőjéről. A metszéspontokat illetően különösen lenyűgözött az, ha egy nagyon egyszerű számítógépes modellel nagyon általános, de komplex jelenségeket tudunk magyarázni. Például egy nagyon egyszerű szabályokat alkalmazó sejtautomata képes akár lavinák, földrengések során felszabaduló energiák eloszlását is megbecsülni. A modelljeink a statisztikus fizika módszereit használják, de sokkal egyszerűbbek és pontatlanabbak, mint a tipikus, biomolekulák viselkedésére kifejlesztett módszerek, cserében viszont gyorsak és általánosíthatók. Pontosan emiatt alkalmazhatók az említett területek metszéspontjain.
S. Z.: Ha ránézek a Google Scholar-profilodra, feltűnik, hogy számos közlésed érintkezik a virológia területével. Fizikusként miért éppen a vírusok váltak számodra fontossá? Modellezhetőség szempontjából ennyire egyedi volna az az ikozaéder alakzat, ami számos vírus proteinhéját jellemzi?
Ty. B.: Tanulmányaim során valahogy sosem volt egy olyan szűkebb tudományterület, amelyre azt mondtam volna, hogy márpedig ezzel akarok foglalkozni. Kevésbé voltam céltudatos, mindig az adott lehetőségeken belül találtam érdekes problémákat. Amikor molekuladinamikai szimuláción dolgozhattam, azt is érdekesnek találtam, amikor pedig arra nyílt lehetőségem, hogy atomerő-mikroszkópon végezzek precíziós méréseket, azt is örömmel megtanultam. Az is szerencsés véletlen, hogy a vírushéjak összeszerelődésével kezdtem foglalkozni. Különböző adminisztratív megszorítások miatt gyakorlatilag egy hét alatt kellett új posztdoktori állást találnom az Egyesült Államokban, és a későbbi mentorom, a Brandeis Egyetemen oktató, kutató Michael Hagan volt olyan elképesztően segítőkész, hogy napok leforgása alatt megszervezte az állásinterjúmat, és segített felgyorsítani az adminisztrációs folyamatot. Ha nem szorít az idő, sosem mertem volna ezt meglépni, mert akkor még fogalmam sem volt az egészről. Ezt vele is közöltem, ennek ellenére megelőlegezte a bizalmat, amiért mindig hálás leszek neki.
Az ismert vírusoknak körülbelül fele ikozaéder alakú, vannak más alakzatúak is, például henger vagy spirál alakúak, ezeket is hasonló módszerekkel modellezzük. Ami különleges az ikozaéderben, az az, hogy magas szimmetriájú, így a legkevesebb típusú elemből létrehozható. Ugyanakkor felszíne a gömbhöz legközelebb álló, így a zárt felületek közül a legjobb a felület–térfogat aránya (adott felületre a legnagyobb térfogatot zárja be). A vírusok szempontjából ez azért jelentős, mert ezek így a legkevesebb típusú és számú proteinből a leghosszabb (legkomplexebb) genetikai anyagot (RNS vagy DNS, vírustól függően) tudják körbezárni, ez a takarékosság pedig a szaporodásuk során evolúciós előnyt biztosít számukra.
S. Z.: Az általad jegyzett közlések szerzőlistáit áttekintve az is feltűnik, hogy gyakran dolgozol biokémikusokkal, vegyészekkel. Mi az előnye ezeknek a transzdiszciplináris kutatócsoportoknak? Mi az, amiben a fizikusnak segítségre van szüksége, amikor azt próbálja megérteni, hogy hogyan lehet a lehető legkevesebb és legkevesebb féle építőanyagból létrehozni egy ikozaédert?
Ty, B.: Inkább megfordítanám a kérdést: azokat a problémákat keresem, amelyek a biokémikusok és vegyészek számára is fontosak. Az érdekel, hogy mivel tudnék én hozzájárulni a megoldáshoz. Az ilyen transzdiszciplináris együttműködések számomra elengedhetetlenek a releváns problémák beazonosításában és az ezekhez kapcsolódó jelenségek megértésében, amelyek alapján aztán a szimulációt fel tudom építeni. Az építőelemek típusának csökkentése is olyan probléma, amellyel a kolloidkísérleteket végző kollégák szembesülnek, hiszen minél több típusú elem szükséges, a kísérlet annál bonyolultabb és költségesebb. A legtöbb ilyen együttműködésem valamilyen formában kötődik a Brandeis Egyetemhez, ahol ezt a munkát elkezdtem.
S. Z.: Jelenlegi tanulmányotok abból az előfeltevésből indul ki, hogy a vírushéjak legnagyobb része, az ikozaéder alakúak „tudnak” valamit, amit mi emberek még nem. Azt „tudják”, hogy miként lehet nagyon takarékosan, a legkevesebb és legkevesebb féle „építőanyagból”, vagyis proteinmolekulából a lehető legnagyobb térfogatú testet felépíteni, amely közrefogja az RNS-t vagy a DNS-t. Ráadásul mindezt egy spontán összerendeződés szabályozza. Mi az, ami ebben a pillanatban határt szab az imént körvonalazott összerendeződés számítógépes modellezésében? Mi az, amit még meg kell értenünk, vagy fel kell tárnunk ebből a folyamatból?
Ty. B.: Ha valóban pontos képet szeretnénk kapni a proteinek viselkedéséről, úgynevezett all-atom típusú szimulációkat kellene alkalmaznunk, amelyekben minden atom térbeli helyzetét nyomon követjük. Ezek rendkívül számításigényesek, több ezer processzoron futtatva is hónapokig tart néhány mikroszekundumos szimulációja egy már létrejött vírushéjnak, az összeszerelődésről – amihez sokkal több elem és hosszabb idő szükséges – már nem is beszélve. A legnagyobb akadályt tehát a véges számítási kapacitás jelenti. Ezért különféle egyszerűsítéseket, közelítéseket kell alkalmaznunk, hogy elfogadható időn belül eredményhez jussunk. Az egyszerűsítések közepette viszont rengeteg részlet elvész, amelyek fontosak lehetnek a teljes folyamat szempontjából. Olyan részletekre gondolok, mint a proteinek pontos térbeli elhelyezkedése, vagy akár a közöttük levő kölcsönhatások bonyolultsága. Azt is mondhatnám, hogy jelenleg egy nagyon rossz felbontású, pixeles képünk van az egész összerendeződési folyamatról, amelyet okos módszerekkel folyamatosan javítani kell, a számítási kapacitás végességét szem előtt tartva.
S. Z.: Ahogy az imént szóba került: van egy analógia a biológiai világból, amely segíthet bennünket takarékos és tartós nanostruktúrák tervezésében és előállításában. Hogyan lehet ezeket a tanulságokat visszavinni, visszafordítani az élettudományok területére? Mit nyerhet ebből például az orvostudomány?
Ty. B.: Valóban, az összeszerelődő szintetikus (tehát nem természetes) nanostruktúrákat a természetben előforduló hasonló folyamatok ihlették. Mivel sok esetben a szintetikus struktúrák jobban kontrollálhatók, általuk mélyebb betekintést nyerhetünk a folyamatba. A folyamat pontos megértése hozzájárulhat különböző gyógyszeres kezelések kifejlesztéséhez, hiszen megtanulhatjuk, melyik fázisban és pontosan hova érdemes célozni ahhoz, hogy az összeszerelődés elromoljon, és a vírusrészecske ne jöhessen létre. Ezt a kérdést vizsgálja részben szimulációs módszerekkel Farzaneh Mohajerani kolléga a Multiscale Modeling of Hepatitis B Virus Capsid Assembly and Its Dimorphism című közös tanulmányunkban.[2]
Egy másik érdekes tanulmányban kollégák úgy terveztek meg szintetikus építőelemeket (háromszögeket DNS-szálból), hogy azok hepatitis B vírusrészecskéket ejtsenek csapdába, így ezek remélhetőleg már nem tudnak szaporodni, tehát fertőzni sem. Látványos, transzmissziós elektronmikroszkópiás képekkel mutatják meg, hogy a módszer működik.[3]
S. Z.: A Magyar Fizika Intézet Facebook-oldalán rövid ismertető jelent meg a tanulmányról, amelyben az alábbi mondat is olvasható: „Kollégánk, Botond Tyukodi és kutatótársai egy olyan algoritmust alkottak, amely a szimmetria elvét használja fel arra, hogy megmutassa: milyen építőelemekből lehet a legegyszerűbben és leghatékonyabban nanostruktúrákat létrehozni”. Hogyan képzelhetem el laikusként, hogy a szimmetria elvére támaszkodtatok?
Ty. B.: Képzeljünk el egy valamilyen építőelemekből összerakott struktúrát, pl. egy egyszínű, ötszög és hatszög alakú foltokból álló futballabdát. Egy testen számos olyan tengely haladhat át, amelyek körül ha a testet elforgatjuk, az nem fedi az eredetit, vagyis nem azt a képet mutatja, amelyet elforgatás előtt láttunk. Vannak ugyanakkor olyan tengelyek, amelyek körül ha elforgatom a labdát, az elfordított labda az eredetit fedi. Ezeket nevezzük szimmetriatengelyeknek. Egy testnek több ilyen szimmetriatengelye is lehet. Most képzeljük el, hogy a labdán minden folt különböző színű. Ez egy nagyon költségesen előállítható labda, hiszen sok (32), különböző színű bőr szükséges hozzá. Ha most az eredeti, kezdetben egyszínű labda valamelyik szimmetriatengelye körül elforgatom ezt a testet, az egymást fedő foltokat egyformára festhetem. Ezáltal csökkentettem a használt színek számát. Ha fokozatosan az összes eredeti tengely körül elforgatom a labdát és az egymást fedő foltokat egyformára színezem, a végén csupán két szín marad, egy az ötszög és egy a hatszög alakú foltoknak. Van tehát egy módszerem arra, hogy fokozatosan eljussak egy nagyon költséges színezéstől egy nagyon takarékos színezésig. Az, hogy melyik színezés működik valójában, szimulációkkal nézzük meg.
S. Z.: „A gond csak az – olvasom ugyanebben az ismertetőben –, hogy minél nagyobb egy ilyen mesterséges szerkezet, annál nagyobb az esélye, hogy hibás formák jönnek létre, ami rontja a hozamot.” Mi az, ami a léptékváltásnál növeli a hibás formák létrejöttének lehetőségét? Mi az, amiben a mágikus méretek, vagyis a nanoszerkezetek világa annyira eltér más léptékű világoktól? Illetve transzponálható-e, és milyen feltételekkel transzponálható mindez más léptékű rendszerekre? Ahogyan egy vírus építkezik, valamilyen módon tanulságos lehet-e egy híd vagy akár egy karbon bicikliváz tervezésében?
Ty. B.: A leglényegesebb különbség a nanoszerkezetek és a makroszkopikus szerkezetek, például egy ház között az, hogy a nanoskálán a hőmérséklet „rendetlenítő” hatása számottevő. Ezen a skálán az építőelemek folyamatos mozgásban, ún. Brown-mozgásban vannak, akárcsak a pollenszemcsék a mikroszkóp alatt. Lebegnek az oldatban, jönnek-mennek, néha találkoznak és egymáshoz tapadnak, máskor újra szétválnak. A struktúra ugyan növekszik, de közben le is esnek elemek róla. Ha az elemeket nem megfelelően tervezzük meg, akkor nem megfelelően csatlakoznak a növekvő struktúrához, és hibák keletkeznek. Pusztán a lehetséges elrendeződések számának növekedése miatt a hiba valószínűsége nagyobb egy nagyobb struktúra esetében. Kisebb, kevesebb elemből álló struktúrákat tehát könnyebb előállítani, mint nagyobbakat.
Nagy hőmérsékleten erőteljes a hőmozgás, és az összetalálkozó elemek nem tapadnak össze. Alacsony hőmérsékleten viszont mind összetapadnak egyetlen, nagy kondenzátummá. Létezik tehát a kettő között egy hőmérsékleti optimum, ahol az összeszerelődés működik, ez az a tartomány, ahol a struktúra lassan növekszik, és az elemek közben le is esnek. A hőmérséklet tehát, bár „rendetlenítő” hatású, elengedhetetlen.
A makroszkopikus rendszereknél a hőmozgás ebben a formában nem releváns. Ha nagyon erős mágneseket szerelek a téglák oldalára és halomba dobálom őket, nem fognak egy szép fallá felépülni, hanem megrekednek egy erősen összetapadó, de rendezetlen rakásban. Nanoskálán az ilyen állapotokat hívjuk kinetikus csapdának, és ebből segíti kilendíteni a rendszert a hőmozgás. A rendezetlen téglarakást erőteljesen össze kéne rázni ahhoz, hogy kilendítsük a csapdából, ez az összerázás lenne a hőmérséklet analógja makroskálán. Azonban egy ilyenfajta összerázás gyakorlati képtelenség. Elméleti analógiaként működhet, de épp az különbözteti meg a két léptéket, hogy makroskálán nincs reális analógiája a már említett hőmérsékleti hatásnak.
S. Z.: A számítógépes szimulációk kimutatták, hogy a hibák elsősorban ott alakulnak ki, ahol bizonyos szimmetriatengelyek csúcsokat metszenek. Ha a tervezés során úgy alakítják ki a héjat, hogy ezek a tengelyek inkább lapokon haladjanak át, a hibák nagy része elkerülhető. Hogyan kell vizuálisan elképzelnünk ezt a javaslatot? Mutatnál példákat? Mit jelent, hogy a szimmetriatengelyek csúcsokat metszenek, és hogyan képzelhető el az a javaslat, hogy a szimmetriatengelyek lapokon haladjanak át?
Ty. B.: A hibák kialakulásának feltétele valóban az, hogy valamely szimmetriatengely valamely csúcsot metssze. A hibáktól tehát kétféleképpen lehet megszabadulni: vagy kiiktatjuk azokat a szimmetriatengelyeket, amelyek csúcsokat metszenek, vagy pedig olyan méretű ikozaédereket választunk, ahol a szimmetriatengelyek lapokon haladnak át.
Az első stratégia költségesebb, hiszen a szimmetriatengelyeket a típusok (a futballabdás pédánál a színek) számának növelésével lehet eltüntetni. A legkevesebb színt felhasználó tervezés lesz a legszimmetrikusabb (itt lesz a legtöbb szimmetriatengely), a legtöbb színt felhasználó pedig a legkevésbé szimmetrikus. A 2 színből varrt futballabdát sokféleképpen el tudom forgatni, hogy önmagát fedje, a 32 színűt egyféleképpen sem.
A második stratégia ezzel szemben teljesen „ingyen” van, és pusztán a geometriából adódik. Ahhoz, hogy ezt megértsük, meg kell vizsgálnunk, hogyan tudunk különböző méretű ikozaédereket előállítani. Az alap ikozaéder 20 egyforma háromszög alakú lapból áll (1.a ábra). Ezeket a lapokat továbboszthatom úgy, hogy minden egyes lap több háromszögből álljon, lásd például a 2.b ábrát, ahol minden ilyen lapot 4 háromszögre osztottam, így négyszer akkora ikozaédert szerkesztettem, mint az alap ikozaéder volt. A szaggatottan jelölt háromszög az alap ikozaéder valamelyik lapját jelöli az 1.a ábrán, illetve az ennek megfelelő továbbosztott lapot az 1.b ábrán.
1. ábra:

A szaggatottan jelölt lap 20 másolatából épül fel az alap ikozaéder (1.a) és a nagyobb ikozaéder (1.b), ez könnyen belátható, ha megvizsgáljuk az alap ikozaéder síkra vetített formáját, amely valóban ugyanazon lap 20 másolatából áll:
2. ábra:

Ezért aztán szerkesztéskor elegendő egyetlen lap viselkedését nyomon követnünk. A lapot 20-szor lemásolva megszerkeszthető a teljes ikozaéder. Egyetlen lapot pedig a következőképpen tudok a legegyszerűbben kisebb háromszögekre osztani: veszek egy háromszögrácsot, és annak bármely két pontját összekötöm egy nyíllal (lásd a 3. ábra piros, zöld és kék nyilait):
3. ábra:
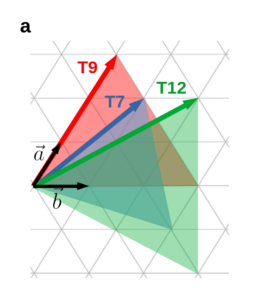
Ezek a nyilak egy-egy egyenlő oldalú háromszög oldalai lesznek, amelyet a háromszögrács által kijelölt kisebb háromszögek alkotnak. Ezek a kisebb háromszögek felelnek meg az építőelemeknek. 20-szor lemásolva (a rács megszorításai mellett) tetszőleges nagyságú ikozaéder előállítható. A számok (T7, T9, T12) azt jelölik, hogy hány építőelemből áll az adott lap, és természetesen az ikozaéder mérete is ezzel arányos. A szerkesztést Don Caspar és Annamaria Klug virológusok vezették be 1962-ben, ez alapján sikerült osztályozniuk struktúrájuk szerint az ikozaéder szimmetriájú vírusokat.
Az így szerkesztett ikozaéderek szimmetriatengelyei ugyanott lesznek, ahol az alap ikozaéderé: a csúcsokon, az élek felezőjénél és a lapok közepén. Az alap ikozaéder szimmetriatengelyeit a 4.a ábrán jelöltem: az élek felezőjénél ellipszissel a kétszeres forgatási tengelyt, a lapok közepén háromszöggel a hármas forgatási tengelyt és a csúcsokon csillaggal az ötös forgatási tengelyt, ezek mind merőlegesek az ábra síkjára. Azonnal látszik, hogyha ezek mentén a 360° 1/2, 1/3, illetve 1/5 részével forgatok, az ikozaéder önmagával átfedésbe kerül. Ugyanezek lesznek a szimmetriatengelyek a nagyobb ikozaédereknél is, viszont lényeges, hogy ezek hogyan kerülnek metszésbe a háromszögrács (azaz az építőelemek) csúcsaival. A 4.b ábrán jól látható, hol haladnak át a szimmetriatengelyek a fentebb megszerkesztett három ikozaéder (T7, T9, T12) esetében. Az ötös tengely minden esetben egybeesik a rácspontokkal a szerkesztés miatt, ez a Caspar-Klug szerkesztés miatt kiküszöbölhetetlen. A kettes és hármas tengely viszont, amint látszik, nem feltétlenül. A T7 esetében egyik sem fed rácspontot, a T9 esetében a hármas fed, a T12 esetében mind a kettes, mind pedig a hármas tengely rácspontot fed.
Ahol egy szimmetriatengely rácspontokat fed, a hibát csak az első stratégiával, a színek számának növelésével, költségesen tudjuk kiküszöbölni. Ahol viszont a szimmetriatengely nem fed rácspontokat, eleve nem jönnek létre hibák, ezekben az esetekben megtarthatjuk a magas szimmetriát (nem kell sok színt használnunk). Azokat a méreteket, ahol sem a kettes, sem pedig a hármas tengely nem esik egybe rácspontokkal, mágikus méreteknek neveztük el, mert ezek nagyon olcsón, hatékonyan előállíthatók, nem szükséges a színek számát nagymértékben növelni. Ilyen méret pl. a T7, T13, T19, vagy T25. Ahol viszont mind a kettes, mind pedig a hármas tengely rácspontokat metsz, azok pocsék méretek, nagyon költségesen állíthatók elő, gyakorlatilag minden alkotóelemet más színűre kell színeznünk. Ilyen például a T12. Még egy tízszer akkora ikozaédert is olcsóbb előállítani, ha az mágikus méretű, mint egy pocsék méretűt. A mágikus és pocsék méretek periodikusan váltakoznak, például a mágikus T13 és a pocsék T12 egymás után következnek, tehát érdemes olyan szomszédos méreteket megcéloznunk, amelyek mágikusak.
4. ábra:

Alább látható két különböző méretű ikozaéder ugyanazzal a szimmetriával. Az elsőnél (5.a) lapon halad át a tengely, a másodiknál (5.b) csúcson.
5. ábra:

S. Z.: Tervezitek folytatni a kutatást? Milyen irányba?
Ty. B.: Reméljük, hogy a kísérleteket végző kutatóknak sikerül ezeket a módszereket DNS-origami háromszögekkel megvalósítaniuk. Ugyanakkor szeretnénk más módszereket/megközelítéseket is kifejleszteni a hibák kiküszöbölésére, a folyamat optimalizálására, és ezeket általánosítani más, nem ikozaéder szimmetriájú felületekre is.
[1] Botond Tyukodi et al.: Magic Sizes Enable Minimal-Complexity High-Fidelity Assembly of Programmable Shells. Physical Review Letters Vol. 135, Iss. 11–12. doi: https://doi.org/10.1103/5yjp-kx2j
[2] Farzaneh Mohajerani et al.: Multiscale Modeling of Hepatitis B Virus Capsid Assembly and Its Dimorphism. ACS Nano 2022 Sep 27;16(9):13845–13859. doi: 10.1021/acsnano.2c02119
[3] Christian Sigl et al.: Programmable icosahedral shell system for virus trapping. Nature Materials 2021 Sep;20(9):1281–1289. doi: 10.1038/s41563-021-01020-4
