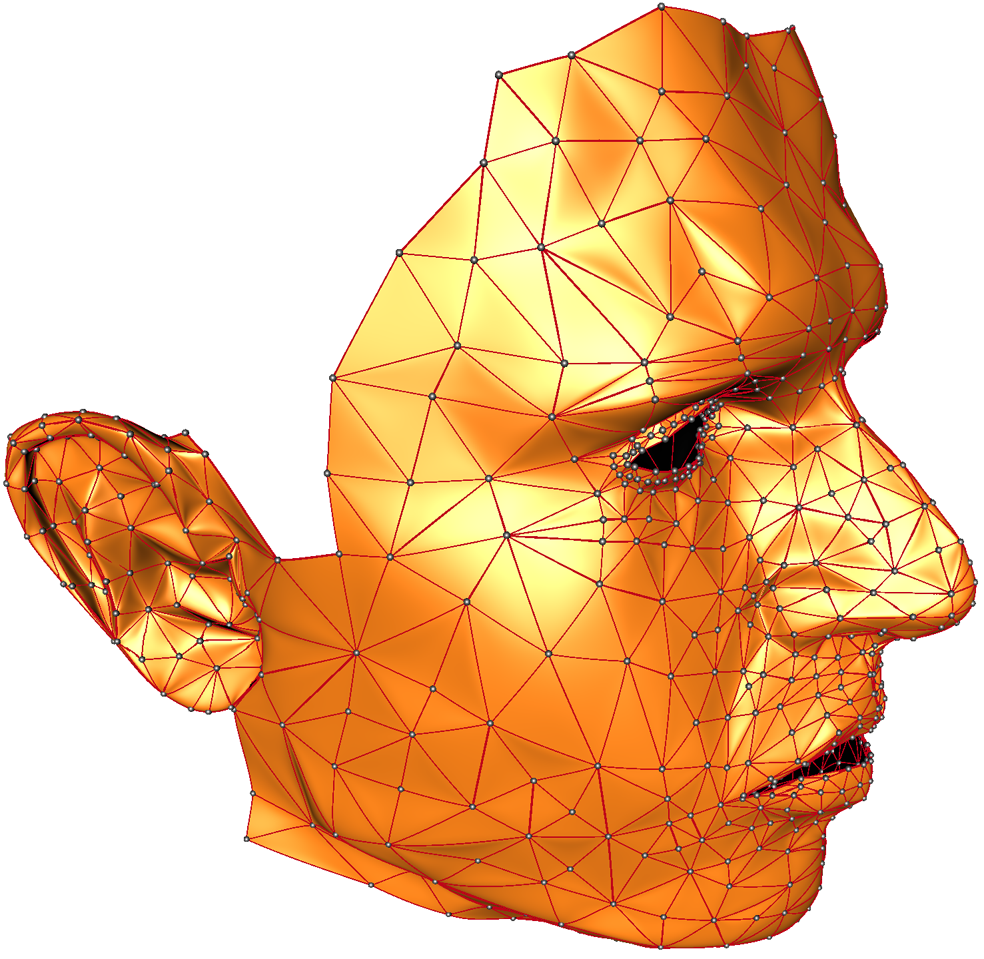
A BBTE Matematika és Informatika Karán oktató-kutató Róth Ágoston szakterülete leginkább a görbe- és felületmodellezéshez, valamint a számítógépi grafikához kapcsolódik. Kutatási irányának alapjai már a középiskolás diákok számára érdekesek lehetnek, hiszen számos geometriához, algebrához, fizikához, programozáshoz kötődő fogalom mélyebb és gyakorlatiasabb megértését teszik lehetővé. A matematikussal Serestély Zalán beszélgetett a szakterületén belül létrejött interdiszciplináris kapcsolódásokról, kutatásainak gyakorlati tétjeiről, a számítógéppel segített geometriai modellezés hazai presztízséről, oktatói módszereiről.
S. Z.: Szakterülete „numerikus analízisre, számítógépi grafikára, számítógéppel segített geometriai modellezésre, Riemann–Finsler-differenciálgeometriai elemekre, differenciálegyenletekre, nemkonvex és nem feltétlenül sima optimalizációs feladatok megoldásait lokalizáló sztochasztikus keresési eljárásokra (például Monte-Carlo-módszerekre és genetikus algoritmusokra) épül”. Ezek általában már összekapcsolt/összefüggő területeknek számítanak, vagy épp Ön próbálja megteremteni az átjárást közöttük?
R. Á.: A felsorakoztatott szakterületek bizonyos értelemben már rég szorosan összefonódnak. Például a (parciális) differenciálegyenletek és az azokból képezett rendszerek a (részecske)fizikában, (égi) mechanikában vagy akár a variációszámításban is természetes módon jelennek meg. Gondoljunk például funkcionálokon értelmezett optimalizációs feladatok megoldását leíró Euler–Lagrange-egyenletekre, Newton második törvényéből fakadó mozgásegyenletekre, különböző távolságfüggvényekkel (metrikákkal) felruházott, valamint görbületváltozás szempontjából nem feltétlenül homogén terek legrövidebb (geodetikus) útvonalainak leírására, optikával, folyadékáramlással, örvényekkel, hő- és hullámterjedéssel kapcsolatos jelenségek, valamint biológiai vagy sztochasztikusan változó folyamatok modellezésére, továbbá stabilitási és egyensúlyi problémák tanulmányozására és jellemzésére.
Nyilván összefüggőségük ellenére az előbb felsorakoztatott szakterületek önálló, mély kutatási témákkal is rendelkeznek. Túlzás lenne azt állítanom, hogy átjárást biztosító hidakat próbálok teremteni a szóban forgó területek között, inkább csak azt mondhatom, hogy a zömében görbe- és felületmodellezéssel kapcsolatos saját kutatási területemen más szakterületek eszköztárát is felhasználom bizonyos feladatok megfogalmazására, tanulmányozására és megoldására úgy, hogy amennyiben lehetséges, ne csak sajátos eseteket tárgyaljak, hanem egyfajta átfogó felülnézetet is biztosíthassak.
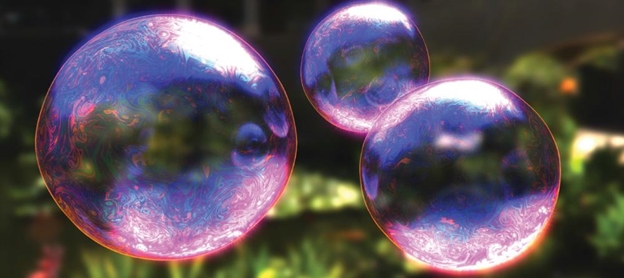
Tegyük fel például, hogy számítógép segítségével légtani hatások miatt folyton deformálódó szappanbuborékok felszínén olajfoltos színjátékú áramlatokat szeretnénk élethűen és valós időben ábrázolni. Ehhez a feladathoz folyadékmechanikára, parciális differenciálegyenletekre, továbbá utóbbiakat hatékonyan megoldó numerikus eljárásokra, mi több programozási készségekre is szükségünk van, annak ellenére, hogy a hétköznapi életben az említett jelenség már gyerekként is oly természetesnek tűnt számunkra.
S. Z.: Melyek a gyakorlati tétjei annak, hogy ezeket a területeket összekapcsoljuk?
R. Á.: Az ezen a területen közölt tudományos dolgozatok gyakorlati haszna kiemelkedő: gondoljunk csak az autó-, hajó- és repülőgépgyártásra, orvostani szövetek vagy érhálózatok megjelenítésére, orvosi műtétekhez szükséges protézisek, illetve mindennapi használati cikkek automatizált előállítására, háromdimenziós képalkotásra és nyomtatásra, felületi rekonstrukcióra, szöveg- és arcfelismerésre, robotkarok és azok illeszkedéseinek mozgásszabályozására, filmiparra, számítógépes játékokra, vagy éppen az építészetre.
S. Z.: Mennyire népszerűek a kutatási területei a hazai kutatók körében? Van-e lehetősége például konzultálni a szakmai dilemmáiról? Vannak-e olyan releváns szakmai fórumok, amelyek segítik a tájékozódásban?
R. Á.: Számítástudományi és matematikai szempontból a kutatási területem leginkább a számítógépi grafikához, illetve a numerikus analízishez kötődik. Utóbbi – különösen az interpolációs és approximációs operátorok, a kvadratúra-képletek, valamint a különféle egyenletrendszerek és egyensúlyproblémák közelítő megoldásának elmélete – viszonylag nagy közkedveltségnek örvend a hazai alkalmazott matematikusok körében.
Viszont úgy érzem, itthon eléggé kevesen művelik a numerikus analízisnek és a számítógépi grafikának azt a sajátos egyvelegét, amivel foglalkozom. Minderről meggyőződhetünk, ha a szaklapokat jegyző nemzetközi adatbázisokból lekérdezzük, hogy hány romániai (társ)szerzős, kimondottan görbe- és felületmodellezéssel vagy számítógépi grafikával kapcsolatos szakdolgozatot közöltek a szóban forgó terület néhány nevesebb szaklapjában (ld. Advances in Applied Mathematics, ACM Transactions on Graphics, ACM Transactions on Mathematical Software, Computer Aided Geometric Design, Computer-Aided Design, Computer Graphics Forum, Constructive Approximation, Journal of Computational and Applied Mathematics) és konferenciakiadványában (ld. Eurographics). Meglepően kevés a találat, annak ellenére, hogy a felsorolt szaklapok több évtizedes múltra tekintenek vissza. Ennek több oka is lehet. Az egyik talán az, hogy – leszámítva az interpolációs és approximációs operátorok, a kvadratúra-képletek, valamint a különféle egyenletrendszerek és egyensúlyproblémák közelítő megoldásának elméletét – ez a kutatási terület nem igazán épült be a hazai doktori iskolák által kínált, numerikus analízishez kapcsolódó témakörökbe. Számítástudományi szempontból pedig egy másik ok a hatékony processzor- és videokártya-alapú, párhuzamosított programozási technikák, valamint az idevágó fejlett adatszerkezetek és algoritmusok ismeretének esetleges hiánya lehet, mert a romániai egyetemeken jelenleg nagyon ritkák az ilyen jellegű kurzusok, szemináriumok és labortevékenységek.
Éppen ezért itthon elenyészőek a kizárólag számítógépi grafikával és geometriai modellezéssel kapcsolatos szakmai fórumok, továbbá kevés olyan személy is van idehaza, akikkel esetlegesen megvitathatnék egy-egy engem érintő szakmai kérdést. Így inkább a szűk nemzetközi kapcsolathálómra támaszkodom. Ettől függetlenül időnként itthon is kialakulhat együttműködési szándék olyan látszólag teljesen különböző szakterületű kutatókkal, akik görbéken vagy felületeken értelmezett optimalizációs feladatokba ütközve – a megoldás esetleges meghatározása és modellezése végett – keresnek meg. Így született például két közös tanulmányunk Kristály Sándorral, aki a BBTE Közgazdaság- és Gazdálkodástudományi Karának Sepsiszentgyörgyi Kihelyezett Tagozatának variációszámítással, differenciálgeometriával, kritikuspont-analízissel és (parciális) differenciálegyenletekkel foglalkozó oktatója és kutatója.
S. Z.: Amikor elkezdett ezekkel a problémákkal foglalkozni, mennyire számítottak bejáratott témáknak a hazai akadémiai közegben, kihez tudott segítségért fordulni?
R. Á.: Középiskolai és egyetemi tanulmányaim alatt tanáraimtól többnyire csak a szakterületem alapeszközeit biztosító ismereteket sajátíthattam el. Ilyenek voltak például az analitikus, affin és projektív geometriát, görbék és felületek differenciálgeometriáját, lineáris algebrát, (parciális) differenciálegyenleteket, valós, komplex és numerikus analízist felölelő kurzusok. Egyetlen rövid félév erejéig számítógépi grafikához kapcsolódó, bevezető alapfogalmakat és módszereket ismertető előadást is látogathattam, ami viszont később évekig meg is szűnt az egyetemünkön. Számos témámhoz kötődő matematikai fogalommal és programozási technikával viszont csak önállóan ismerkedhettem meg. Ilyenkor az egyetemi könyvtárban fellelhető szakkönyvek és az internet számított kiváló forrásanyagnak. Úgy gondolom, hogy kutatási témám jelenleg sem tekinthető kiforrott irányvonalnak a hazai akadémiai közegben. Egyrészt még nekem is sokat kell fejlődnöm, másrészt pedig sokkal többen fel kellene vállalnunk ezt a témakört, hogy ilyen irányú életképes mesterszakot és doktori képzést ajánlhassunk a diákjaink számára.
S. Z.: Melyek a lehetőségfeltételei az Ön által végzett kutatásoknak? Milyen felszerelést igényelnek? A rendelkezésre álló kutatási infrastruktúra, a támogatási lehetőségek és a támogatások természete mennyire határolja be a kutatás irányát, intenzitását?
R. Á.: Bizonyos szintig viszonylag könnyen megteremthetők az ilyen típusú kutatásokat biztosító infrastruktúra alapfeltételei. Néhány kiváló szakkönyvre és tanulmányra támaszkodva, papírt és írószert használva, továbbá egy jobb processzorral, komolyabb videokártyával és kellő memóriával rendelkező számítógépet hatékonyan programozva, elvileg már elkezdhetők lennének a kutatások. Infrastruktúra szempontjából itthon akkor jelentkeznek gondok, amikor további segédeszközökre, például többmagos numerikus társprocesszorokra, holovíziót használó, háromdimenziós megjelenítőre, háromdimenziós nyomtatóra, virtuális valóság bejárására és programozására használható szemüvegre, mozgásérzékelőkre, esetleg lézer alapú távérzékelést biztosító eszközökre lenne szükségünk. Egyáltalán nem biztos, hogy a felsőoktatási intézményünk ilyen igényekre anyagi keretet tud biztosítani. Ilyen speciálisabb segédeszközöket csak hazai vagy külföldi kutatási pályázatok esetleges elnyerésével tudunk beszerezni, s még ha sikerül is nyertes pályázatot írni, a termékek beszerzése több hónapig vagy akár évekig is elhúzódhat a hazai bürokrácia miatt.
S. Z.: Ha jól értem, a matematikának ezek a területei már jócskán átnyúlnak a programozásba? Ez a tény mennyire teszi „piacossá”, eladhatóvá a kutatásait? Mit tapasztal, van irántuk kereslet a magánszektor irányából, vagy ennél azért teoretikusabb szinteken mozognak?
R. Á.: A kutatási eredmények szemléltetése és azok gyakorlati hasznának kidomborítása végett ezen a területen valóban szükség van fejlett programozási technikákra is. Annak ellenére, hogy úgy érzem, lenne akár tényleges ipari felhasználhatósága a kutatási eredményeimnek, a tapasztalataim szerint a magánszektor inkább a már több évtizede szabványként használt, (racionális) nem feltétlenül egyenletes csomóvektorú B-spline-görbéket és felületeket részesíti előnyben.
S. Z.: Az Ön által végzett munka számos ponton érintkezik a vizualitással. A vizuális kultúra kizárólag matematikai értelemben foglalkoztatja, vagy más szinteken is szerepet játszik az életében? Egyáltalán van olyan típusú vizualitás, ami nem érintkezik a matematikával?
R. Á.: Úgy gondolom, a kultúra – bármilyen jellegű is legyen – tudást, művészetet, hagyományt, törvényeket, hétköznapi képességeket, szokásokat, hitet és akár hiedelmeket is magába foglal,és talán mindennek a látáshoz kapcsolódó részét nevezném vizuális kultúrának. Környezetünkben számos (vizuális) jelenség lefordítható fizikai, biológiai és kémiai folyamatok matematikával átitatott nyelvezetére, de kétlem, hogy például egy művész/mérnök/tervező az alkotás pillanatában végig matematikai precizitással gondolkodna, hacsak nem pont ez az eltökélt szándéka. A mű lelkét formáló (virtuális) ecsetet azért ösztönös érzéssel is húzni kell.
S. Z.: Mennyire lehet összeegyeztetni a kutatásait az oktatással? Úgy tudom, a diákjai élvezettel hallgatják az óráit.
R. Á.: Az óráimon elhangzott elméleti részeket általában saját fejlesztésű, saját kutatási eredményekre épülő interaktív alkalmazások segítségével szemléltetem. Előfordulhat, hogy a bemutatott alkalmazások hátterében rejlő elméleti eszköztárat a diákjaim az addigi tanulmányaik alapján még nem ismerik, vagy még nem teljesen látják át, de tapasztalataim alapján az új fogalmak látványszerű érzékeltetése mindenképpen segít azok elmagyarázásában és megértetésében. Továbbá az általam ajánlott szakdolgozat- és disszertációtémák is a kutatási eredményeimhez kötődnek. Ha valaki tanulmányainak lezárásaként ilyen jellegű témát választ, akkor egyrészt a dolgozataimban megjelenő matematikai eszköztár megértését, másrészt pedig az azokban megjelenő görbe- és felületmodellezéssel kapcsolatos módszerek hatékony kódolását is vállalnia kell.
S. Z.: Esetleg el tud képzelni olyan módszereket, amelyek már középiskolás korban hozzáférhetővé, gyakorolhatóvá tennék a számítógéppel segített geometriai modellezést?
R. Á.: Szerintem számos középiskolás diák képzeletét lebilincseli a számítógépi grafika és a geometriai modellezés. Az egyetemi oktatás során minden évfolyamon találkozok olyan hallgatókkal, akik már középiskolás korukban megpróbáltak akár önállóan is elsajátítani idevágó matematikai fogalmakat, programozási adatszerkezeteket és technikákat. Nekem például tizedikes koromban került a kezembe az első számítógépi modellezéssel kapcsolatos szakkönyv, és annak ellenére, hogy voltak benne olyan fogalmak, amelyek csak egyetemi tanulmányaim során tisztázódtak bennem, mégis megpróbáltam megérteni és gyakorlatba ültetni a könyvben bemutatott görbe- és felületmodellezési eljárásokat. A diákok érdeklődését könnyen fel lehetne csigázni ezzel a témakörrel, ehhez viszont nemcsak matematika- és informatikatanárok erőfeszítése, hanem a szülők biztató hozzáállása is szükséges. Én sokáig csak az ábrákat lapozva szemeztem az otthoni könyvesboltban az említett könyvvel, míg rávettem a szüleimet, hogy vegyék azt meg nekem, hogy kipróbálhassam a módszereket az akkori 1 megabyte-os videokártyájú, 100 megahertzes számítógépünkön. A mostani számítógépi grafika és geometriai modellezés műveléséhez viszont már lényegesen komolyabb videokártyával és processzorral rendelkező hardver szükséges, amelynek beszerzéséhez elengedhetetlen a szülői támogatás. Az ilyen jellegű témák szakkörökön történő, középiskolai szintű bemutatása számos geometriához, analízishez, lineáris algebrához, fizikához, valószínűség-számításhoz, algoritmikus gondolkodáshoz, programozáshoz és adatszerkezetekhez kötődő fogalom mélyebb és gyakorlatiasabb megértését tenné lehetővé. Ha pedig valakit esetleg nem is érdekel, hogy milyen matematikai vagy programozási eszköztár húzódik meg egy-egy módszer hátterében, hanem egyszerűen művészi indíttatásból szeretne modellezni, a https://www.blender.org/ linken elérhető, szabad, nyílt forráskódú, Blender háromdimenziós grafikai tervezőprogram kipróbálását ajánlanám (bár meggyőződésem, hogy csak akkor látunk be a színfalak mögé, ha a miértekre is válaszolni tudunk).
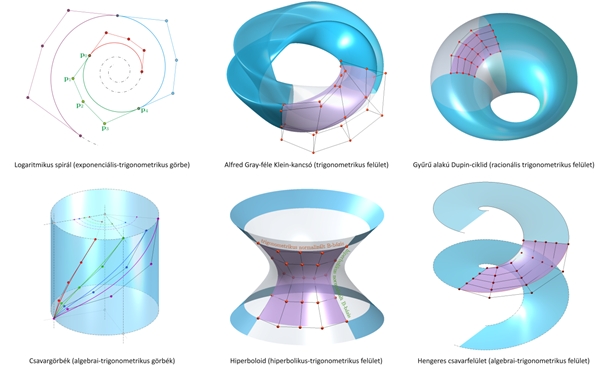
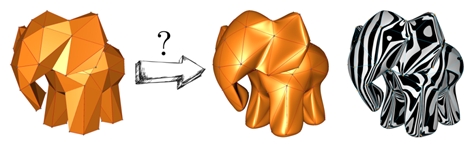
Az alábbi képek a Róth Ágoston által fejlesztett programok segítségével készültek:
Irodalomjegyzék
J. Hill, R. D. Henderson, 2016. Efficient fluid simulation on the surface of a sphere, ACM Transactions on Graphics, Vol. 35, Nr. 2, Article 16.
Kristály, Gh. Moroşanu, Á. Róth, 2008. Optimal placement of a deposit between markets: a Riemann-Finsler geometrical approach, Journal of Optimization Theory and Applications, 139(2):263–276.
Kristály, Á. Róth, May 15–17, 2014. Testing metric relations on Finsler manifolds via a geodesic detecting algorithm, In 9th International Symposium on Applied Computational Intelligence and Informatics (SACI), Institute of Electrical and Electronics Engineers, Timișoara, pp. 331–336.
Á. Róth, 2015. Control point based exact description of curves and surfaces in extended Chebyshev spaces, Computer Aided Geometric Design, 40:40–58.
Á. Róth, 2016. Nielson-type transfinite triangular interpolants by means of quadratic energy functional optimizations, https://arxiv.org/abs/1604.01910.
Á. Róth, 2019. Algorithm 992: An OpenGL- and C++-based function library for curve and surface modeling in a large class of extended Chebyshev spaces, ACM Transactions on Mathematical Software, Vol. 45, No. 1, Article 13.